Heap Sort
Traversal in Binary Tree：

將陣列中的數值依據根節點、父節點、子節點來進行排序(升冪、降冪)，
其中根節點為該陣列數值中的最大值，
依序父節點大於子節點排序。

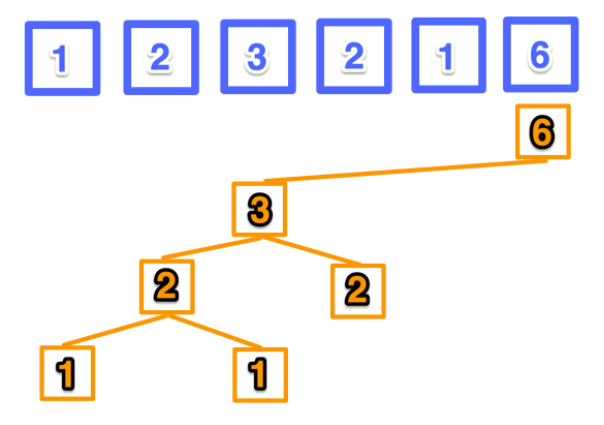
Input: nums = [1, 2, 3, 2, 1, 6]

let heapSort = (nums) => {
  function heapify(nums, length, node) {
    const left = node * 2 + 1
    const right = node * 2 + 2

    let max = node

    if (left < length && nums[left] > nums[max]) max = left
    if (right < length && nums[right] > nums[max]) max = right

    if (max !== node) {
      [nums[node], nums[max]] = [nums[max], nums[node]]
      heapify(nums, length, max)
    }
  }

  const length = nums.length

  for (let i = Math.floor(length / 2) - 1; i >= 0; i--) {
    heapify(nums, length, i)
  }

  for (let i = length - 1; i > 0; i--) {
    [nums[0], nums[i]] = [nums[i], nums[0]]
    heapify(nums, i, 0)
  }
  return nums
}

Output: newNums = [1, 1, 2, 2, 3, 6]

Flow Chart:

0: heapify(nums, length, max)
1: heapify(nums, length, i)
2: heapify(nums, i, 0)

0: [ 1, 2, 6, 2, 1, 3 ] 6 5
1: [ 1, 2, 6, 2, 1, 3 ] 6 2
1: [ 1, 2, 6, 2, 1, 3 ] 6 1

0: [ 6, 2, 3, 2, 1, 1 ] 6 5
0: [ 6, 2, 3, 2, 1, 1 ] 6 2
1: [ 6, 2, 3, 2, 1, 1 ] 6 0

0: [ 3, 2, 1, 2, 1, 6 ] 5 2
2: [ 3, 2, 1, 2, 1, 6 ] 5 0

0: [ 2, 2, 1, 1, 3, 6 ] 4 3

0: [ 2, 2, 1, 1, 3, 6 ] 4 1
2: [ 2, 2, 1, 1, 3, 6 ] 4 0

0: [ 2, 1, 1, 2, 3, 6 ] 3 1
2: [ 2, 1, 1, 2, 3, 6 ] 3 0
2: [ 1, 1, 2, 2, 3, 6 ] 2 0
2: [ 1, 1, 2, 2, 3, 6 ] 1 0

[ 1, 1, 2, 2, 3, 6 ]

Blog：http://52.198.119.162/關於heap-sort排序方法與示意圖/